elliptic: Weierstraß elliptic functions

Hi the lonely reader :)

Trying to conclude the elliptic package I have to pass one very complicated stair. This the Weierstraß elliptic function ℘. The theory you can find here

   http://en.wikipedia.org/wiki/Weierstrass_elliptic_function

Here are just my plans to afford the task. Since the Weierstrass's elliptic function ℘ posses one very nice representation in terms of theta functions.
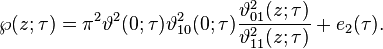
   $\wp(z; \tau) = \pi^2 \vartheta^2(0;\tau) \vartheta_{10}^2(0;\tau){\vartheta_{01}^2(z;\tau) \over \vartheta_{11}^2(z;\tau)} + e_2(\tau).$
where
      $e_1(\tau) = {\pi^2 \over {3}}(\vartheta^4(0;\tau) + \vartheta_{01}^4(0;\tau)),$
   $e_2(\tau) = -{\pi^2 \over {3}}(\vartheta^4(0;\tau) + \vartheta_{10}^4(0;\tau)),$
   $e_3(\tau) = {\pi^2 \over {3}}(\vartheta_{10}^4(0;\tau) - \vartheta_{01}^4(0;\tau)).$

are the roots of the equation X³ − g₂X − g₃ where g₂ and g₃ are invariants and depend only on τ, being modular forms.

The another approach (always citing the wiki page) is to calculate the Weierstrass elliptic function in terms of the Jacobi's elliptic functions. The basic relations are
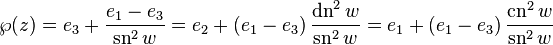
         $\wp(z) = e_{3} + \frac{e_{1} - e_{3}}{\mathrm{sn}^{2}\,w} = e_{2} + \left( e_{1} - e_{3} \right) \frac{\mathrm{dn}^{2}\,w}{\mathrm{sn}^{2}\,w} = e_{1} + \left( e_{1} - e_{3} \right) \frac{\mathrm{cn}^{2}\,w}{\mathrm{sn}^{2}\,w}$
where e_1-3 are the three roots described above and where the modulus k of the Jacobi functions equals

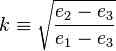
$k \equiv \sqrt{\frac{e_{2} - e_{3}}{e_{1} - e_{3}}}$